
문제
4485번: 녹색 옷 입은 애가 젤다지?
젤다의 전설 게임에서 화폐의 단위는 루피(rupee)다. 그런데 간혹 '도둑루피'라 불리는 검정색 루피도 존재하는데, 이걸 획득하면 오히려 소지한 루피가 감소하게 된다! 젤다의 전설 시리즈의 주
www.acmicpc.net
간단한 문제 요약
'도둑루피' 라는 검정색 루피를 획득하면 소지한 루피가 감소한다. N*N의 동굴에는 도둑 루피로 가득하다. 젤다는 [0][0]위치에 있고 출구는 맨 아래칸 [N-1][N-1]로 이동해야한다. 동굴의 각 칸은 도둑 루피가 있다. 잃는 금액을 최소로 해서 동굴의 출구로 이동해야 한다. 한번에 한 칸 이동할 수 있다.
고려해야 할 사항
- 도둑 루피 크기가 K인 특정 칸을 지나면 K루피를 잃는 다는 뜻
- 시작점 [0][0]
- 도착점 [N-1][N-1]
문제 풀이
기존에 풀었던 문제는 startVertex endVertex cost로 이루어진 input이었다. 지금은 2차원 배열로 vertex가 주어졌고 배열에 존재하는 값은 도둑루피라 불리는 'cost'가 있다.
typealias Point = (x:Int,y:Int)
struct Node {
let point: Point
let cost: Int
var x: Int {
return point.x
}
var y: Int {
return point.y
}
}
extension Node: Comparable {
static func <(lhs: Node, rhs: Node) -> Bool {
return lhs.cost < rhs.cost
}
static func ==(lhs: Node, rhs: Node) -> Bool {
return lhs.x == rhs.x && lhs.y == rhs.y
}
}
x,y좌표를 갖고 cost를 갖는 Node구조체를 이용해서 우선순위 큐의 Element type로 지정 했습니다. 초기 visited는 Int.max로 값을 세팅했습니다.

visited는 측정 구간을 방문했을 때 저장된 최소 비용이 들어가 있는 배열입니다. map은 도둑루피 값이 저장된 값 입니다.
for (dx,dy) in Direction {
let (nx,ny) = (curNode.x+dx,curNode.y+dy)
if isOutOfBound(point: (nx,ny), n: n) { continue }
if visited[ny][nx] > curNode.cost + map[ny][nx] {
visited[ny][nx] = curNode.cost + map[ny][nx]
priority.insert(Node(point: (nx,ny), cost: visited[ny][nx]))
}
}출발점인 [0][0]의 cost는 0으로 하고 맵의 상 하 좌 우를 탐색하면서 이전에 기록된 visited의 cost보다 현재 특정 칸을 통해 새롭게 더해진 cost값이 낮을 경우 해당 visited를 갱신합니다.

그 예로 [0][1]의 새로운 칸을 탐색할 때 기존에 있는 cost (Int.max) 가 큰지 현재 칸의 누적된 cost + 새로운 칸[0][1]을 탐색했을 때의 cost 70을 더한 값이 작은지를 비교한 후 visited 값을 새로 갱신합니다.
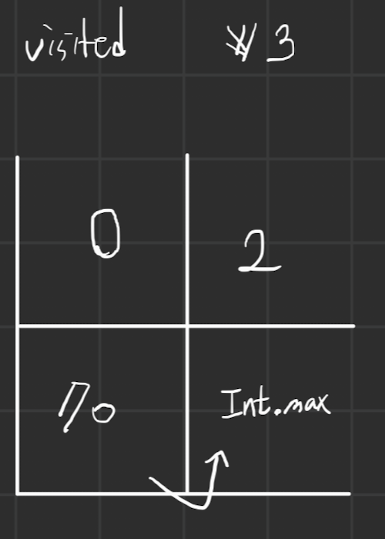
visted[1][1]의 값을 갱신하는 것을 예로 들었을 때 현재 저장된 visted[1][1]의 cost 인 Int.max가 작은지, 현재 특정 칸[0][1]에서
[1][1]로 갈때의 map[1][1]값(3)을 더한 값이 작을지 비교합니다. if visited[1][1] value > visited[0][1] + map[1][1]value { vistied[1][1]값 새로 갱신 }
우선순위 큐를 사용했습니다. 시간 복잡도를 단축할 수 있습니다.
코드
solution
func isOutOfBound(point: Point, n: Int) -> Bool {
return point.x < 0 || point.x > n - 1 || point.y < 0 || point.y > n - 1
}
func dijkstra(map : inout [[Int]],visited : inout [[Int]], n: Int) {
var priority = Heap<Node>()
priority.insert(Node(point: (0,0), cost: 0))
visited[0][0] = 0
while !priority.isEmpty {
guard let curNode = priority.delete() else {
return
}
if visited[curNode.y][curNode.x] < curNode.cost {
continue
}
for (dx,dy) in Direction {
let (nx,ny) = (curNode.x+dx,curNode.y+dy)
if isOutOfBound(point: (nx,ny), n: n) { continue }
if visited[ny][nx] > curNode.cost + map[ny][nx] {
visited[ny][nx] = curNode.cost + map[ny][nx]
priority.insert(Node(point: (nx,ny), cost: visited[ny][nx]))
}
}
}
}
func solution() {
var idx = 1
while true {
let n = Int(readLine()!)!
if n == 0 { break }
var map = Array(repeating: [Int](), count: n)
var visited = Array(repeating: Array(repeating:Int.max, count:n), count: n)
(0..<n).forEach{ i in
map[i] = readLine()!.split{$0==" "}.map{Int(String($0))!}
}
dijkstra(map: &map, visited: &visited, n: n)
print("Problem \(idx): \(map[0][0]+visited[n-1][n-1])")
idx += 1
}
}
solution()Model
typealias Point = (x:Int,y:Int)
struct Node {
let point: Point
let cost: Int
var x: Int {
return point.x
}
var y: Int {
return point.y
}
}
extension Node: Comparable {
static func <(lhs: Node, rhs: Node) -> Bool {
return lhs.cost < rhs.cost
}
static func ==(lhs: Node, rhs: Node) -> Bool {
return lhs.x == rhs.x && lhs.y == rhs.y
}
}
let Direction = [(-1,0),(1,0),(0,1),(0,-1)]heap
struct Heap<T> where T: Comparable {
private var list = [T]()
private let isLeftSmall: (T,T) -> Bool
var isEmpty: Bool {
return list.isEmpty
}
var count: Int {
return list.count
}
init(isLeftSmall: @escaping (T, T) -> Bool) {
self.isLeftSmall = isLeftSmall
}
init() {
self.init(isLeftSmall: <)
}
}
extension Heap {
mutating func insert(_ element: T) {
var idx = list.count
list.append(element)
while idx > 0 && isLeftSmall(list[idx], list[(idx-1)/2]) {
list.swapAt(idx, (idx-1)/2)
idx = (idx-1)/2
}
}
mutating func delete() -> T? {
guard !isEmpty else {
return nil
}
guard count != 1 else {
return list.removeFirst()
}
let element = list.first!
var idx = 0
list.swapAt(idx, list.count-1)
_ = list.removeLast()
while idx < list.count {
let (left,right) = (idx*2+1,idx*2+2)
if right < count {
if isLeftSmall(list[left],list[right]) && isLeftSmall(list[left], list[idx]) {
list.swapAt(left, idx)
idx = left
} else if isLeftSmall(list[right], list[idx]) {
list.swapAt(right, idx)
idx = right
}else {
break
}
} else if left < count {
if isLeftSmall(list[left], list[idx]) {
list.swapAt(left, idx)
idx = left
} else {
break
}
} else {
break
}
}
return element
}
}힙을 구성할 때 comparer를 썼을 때 간혹 했갈려서 의미를 명확하게 부여했더니 파악하기 쉬워졌습니다.
'백준 PS일지 > Dijkstra' 카테고리의 다른 글
| [백준/Swift] 11779: 최소비용 구하기 PS일지 (0) | 2023.01.11 |
|---|---|
| [백준/Swift] 1504: 특정한 최단 경로 (0) | 2023.01.09 |
| [백준/Swift] 1261: 알고스팟 (0) | 2023.01.08 |
| [백준/Swift] 1238 : 파티/ 우선순위 큐 개념 정리, 최소 힙 개념 with 라이노님 Heap 정리 (2) | 2023.01.06 |



