https://www.acmicpc.net/problem/1025
1025번: 제곱수 찾기
첫째 줄에 N, M이 주어진다. 둘째 줄부터 N개의 줄에는 표에 적힌 숫자가 1번 행부터 N번 행까지 순서대로 한 줄에 한 행씩 주어진다. 한 행에 적힌 숫자는 1번 열부터 M번 열까지 순서대로 주어지
www.acmicpc.net
1025 : 제곱수 찾기 / 문제 소개
N행 M열의 표의 각 칸에는 숫자가 한개 씩 있다.
서로 다른 1개 or 1개 이상의 칸을 선택 하려고 한다.
이때, 칸을 선택할 수 있는 조건이 있다.
특정칸에 위치하는 행이 등차수열을 이루어야한다. 열 또한 등차수열을 이루어야 한다.
위의 조건을 만족하는 칸을 고를 때 그 순서대로 '정수'를 만들 수 있다. 이때 구할 수 있는 가장 큰 완전제곱수(우리가 선택해서 만든 정수 중 해당 정수가 제곱수여야 함과 동시에 N행 M열에서 만들 수 제곱수들 중 가장 큰 제곱수)
등차수열은 쉽게 말해 연속하는 두 항의 차이가 일정한 수!!( == d ) 를 말한다.
즉
- 1, 1, 1, 1, 1 이라는 수는 차이가 0으로 연속적인 등차수열에 포함된다.
- 1, 2, 3, 4, 5 이 숫자들 또한 차이가 +1으로 연속적인 등차수열에 포함된다.
- 1, 3, 5, 7, 9 이 숫자들 또한 차이가 +2으로 연속적인 등차수열에 포함된다.
N행 M열에서 이러한 등차수열의 규칙을 조건으로 특정한 칸 or 여러개의 칸을 선택 할 수 있는 것이다.
예를들어
input
2 3
123 (0,0)(1,0)(2,0)
456 (0,1)(1,1 )(2,1)
이 주어졌다.
만들 수 있는 정수는?
행에서의 d = 0일 때 열에서의 d = 0 일 때 1, 2, 3, 4, 5, 6 이 나올 수 있다.
행에서의 d = 0이고, 열에서의 d = 1 일 때 12, 25, 36 이 나온다.
이런식으로 행에서 등차수열의 규칙을 적용하고 && 열에서 등차수열의 규칙을 적용하면 조건에 만족되는 숫자들을 선택 할 수 있다.
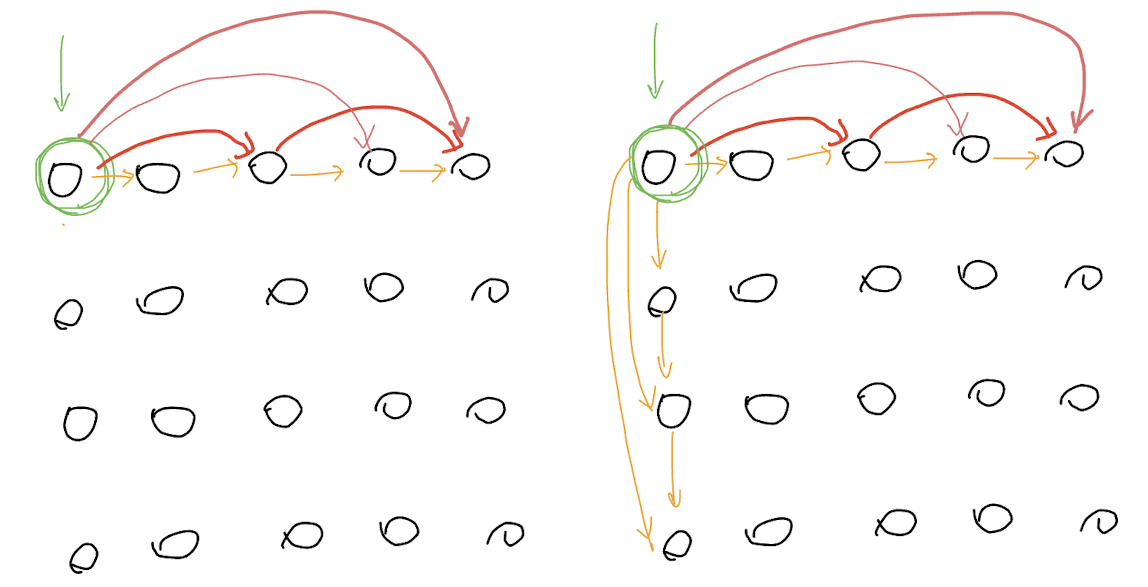
그림1 의 왼쪽 그림을 보면
우선 (0,0)을 기준으로 만들 수 있는 숫자들을 보자!!
열의 공차는 0이라고 가정한다면
행에서 나올 수 있는 등차수열의 공차는 0, 1,2,3 이 있다.
공차 d 가
- 0일때는
(0,0)이 수가 정수가 되고
- 1일때는
(0,0) (1,0)
(0,0) (1,0) (2,0)
(0,0) (1,0) (2,0) (3,0) 이렇게 3개의 좌표에 써져있는 3개의 숫자들이 정수가 된다.
- 2 일때는
(0,0) (2,0)
- 3일때는
(0,0) (3,0)
고렇다면 여기서 퀴즈!!
(0,0) (1,0) (3,0) 세개의 좌표를 선택하면 왜 안돼는가?
??
0,0 에서 1,0은 행의 공차가 1이다. 근데 1,0에서 3,0은 행의 공차가 2이다.
두 항의 차이 (d)가 일정한 수열을 의미하는데 위의 좌표는 1과 2. 즉 등차수열이 될 수 없다. 따라서 3개의 좌표를 선택할 수 없다.
(0,0) (1,0) 을 선택하거나 (0,0) (3,0) 또는 (1,0) (3,0) 또는 (3,0) (1,0) 또는 (3,0) (0,0) 또는 (1,0 ) (0,0)등 이 선택될 수 있다.
그림 1 뿐 아니라 (0,0)에서 만들 수 있는 정수는 다양하다.

그래서 문제를 풀 당시 나는 위의 규칙을 적용해 특정한 칸을 기준으로 나올 수 있는 정수들을 화살표로 그려봤다.

;;
이를 어떻게 포문으로 훑는단 말인가?
빨간색의 경우 나올수 있는 정수는 검정색 으로 표시한 것들이다. 그뿐만 이 아니라 빨간색을 1,1이 아니라 2,1에서 그린 경우에도 오른쪽이나 대각 왼쪽 아래 대각오른쪽으로 숫자들을 만들 수 있다. 그 뿐 아니다.
초록색 동그라미(5,1)의 경우 다시 1,1까지 탐색을 해나가야한다.
(5,1)에서 (1,1)? 이땐 공차가 -4이다.
풀이 과정
위에서 그린 그림3에서
처음 선택한 좌표가 빨간색 일때,
연속된 행과 열의 공차는 각각 0~3이 될 수 있다.
또한 처음 선택한 좌표가 초록색 일 때 연속된 행과 열의 공차는 각각 -3 ~ 0이 될 수 있다.
일단 빨간색에서 맨 끝의 행 열을 탐색하기 위해서는 이중 포문이 필요하다.
그 각각의 선택된 처음 좌표에 대해서!!!!
연속된 행과 열의 공차를 적용하면 된다.
위에서 그린 그림3에서 이때(1,1) 의 경우 선택될 수 있는 행 열의 공차는 다 양수여야하지만,
(2,1)일때 ... (5,1)일 때는 음수의 공차가 필요하다.
또한 공차 d = 0일때 한개의 선택된 정수 또한 완전 제곱수가 될 수 있는걸 유의해서 코드를 구현해 나가면 된다.
여기서 처음에 그럼 이 경우의 연속된 숫자들을 어딘가에 저장해야 하는것 아닌지? 하면서 풀어갔는데
예를들어 (0,0)에서 열의 d = 0, 행의 d = 1 일 때는 선택될 수 있는 수가 (0,0) 과 (0,0) (1,0) 이고 이 두개에서 뒤에 값을 더 붙인 (0,0) (1,0) (2,0) 이런식으로 이전 에 구한 정수가 필요하기 때문에 구한 즉시 완전 제곱수인지를 구하면서 그 값을 저장하고, 새로운 좌표가 추가될 때 완전 제곱수인지를 판별해 가면 되는 문제이다.
코드 구현
import Foundation
func BOJ_1025()
{
let rect = readLine()!.split(separator:" ").map{Int($0)!}
let height = rect[0]
let width = rect[1]
var map = Array(repeating:[String](),count: height)
var res = -1
for i in 0..<height
{
map[i] = readLine()!.map{String($0)}
}
/*
여기서 생성되는 (x,y)좌표는 그림3에서 빨간색 점 부터~ 초록색점 ~ 맨 끝 (4,4)의 점까지 탐색하기
위한 2중 포문이다. 즉 이 포문을 통해 (0,0) 일 때 나올 수 있는 모든 정수들 중 완전 제곱수(최대값을 갖는 제곱수)를 찾는 즉시 갱신해 갈 것이다.
*/
for y in 0..<height
{
for x in 0..<width
{
/*
여기서 나올수 있는 공차를 구해야한다. 이때 주의할 점이
N M 행열의 좌표들은 양수이다.
따라서 특정한 좌표에 연속적인 등차수열을 구하기 위해 각각의 행 열에 공차를 더할 때
그 행, 열의 좌표가 음수이면 탐색을 못하도록 while문에 조건을 달아야한다!!
*/
for dy in (-(height-1))..<height
{
for dx in (-(width-1))..<width
{
var curX = x
var curY = y
var sum = 0
var strSum = ""
while (curX >= 0 && curX < width) && ( curY >= 0 && curY < height)
{
strSum += map[curY][curX]
sum = Int(strSum)!
var sqrtNum = Int(sqrt(Double(sum)))
if sqrtNum*sqrtNum == sum
{
res = max(res, sum)
}
if dx == 0 && dy == 0
{
break
}
curX = curX + dx
curY = curY + dy
}
}
}
}
}
print(res)
}
BOJ_1025()
visit my github

'백준 PS일지 > BruteForce' 카테고리의 다른 글
| [백준/Swift] 사탕 게임: 3085 | PS일지 (0) | 2023.05.09 |
|---|---|
| [백준/Swift] 2475: 검증수 (0) | 2023.02.16 |
| [백준/Swift] 2231 : 분해합 (0) | 2022.04.30 |
| [백준/Swift] 1018 : 체스판 다시 칠하기 (0) | 2022.04.30 |



