https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
10844 : 쉬운 계단 수 / 문제 소개
문제
45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.
입력
첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
풀이 과정
처음에 문제를 봤을 때 N==2일땐 인접한 모든 자리 차이가 2인 수를 뜻하는줄알았다. 10 이상일땐 어찌된다는말인가? ...
알고보니
계단수란 인접한 모든 자리의 차이가 1인 수를 의미한다. ㅋㅋㅋ...
N은 자리 숫자이다. 최대 100자리까지 만들 수 있음을 의미한다.
단 0으로 시작하는 수는 계단수가 아니다!!
그렇다면
| num | N==1일 때 |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
N == 2일 때는 이전에 구했던 N == 1일때의 num뒤에 각각 +1 또는 -1을 한 양의 정수를 더한다면 계단수가 만들어진다.
1을 예로 든다면
- N == 1일 때
1
- N == 2일 때
10
12
- N == 3일 때
101
121
123
- N == 4일 때
1010
1012
1210
1212
1232
1234
이런식으로 된다. 이전값에 따라 뭔가 패턴이 보이긴 한다.

지금은 N == 2일 때를 구한것인데
N ==1인 경우의 각각의 1,2,3,4,5,6,7,8,9에 대해서!!!
N==2의 계단 수를 구한 것이다.
01은 안 돼? 네 안됩니다. 계단수는 0부터 시작하지 않기 때문입니다.
이 그림을 다시 잘 보면 N==2에서
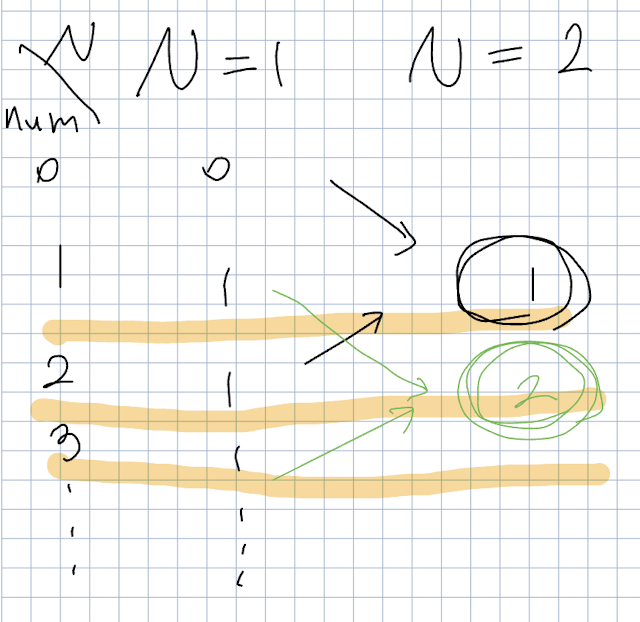
각각 동그라미 친 N==2일 때 뒤의 자리가 1을 갖는 숫자, 2를 갖는 숫자 모두 이전에 구한 N==1일때 위 아래 value를 더해서 구하면 값이 나온다는 것이다.
그림 1은 나올 수 있는 숫자를 구한 것이고,
그림2는 나올 수 있는 숫자의 개수를 구한 것이다.
다시 여기서 그림1의 num == 0과 9일 때를 보면 각각 한개만 계단 수를 구할 수 있다.
그외의 나머지들은 두개씩의 계단수를 갖는다.
그림 2를 생각하며 N==3일 때 각각 num에 따라 구할 수 있는 계단수를 구하면 이전에 구한 계수만큼을 더해주면 된다.

요런 느낌으로 패턴을 구할 수 있다.
이를 이제 코드로 구현하면 된다.
주의할 점은 1,000,000,000으로 나누어야 한다.
코드 구현
import Foundation
/*
이 문제는 계단을 더해갈때 % 1,000,000,000 하지 않고 n=100일때 구하면 n=68번째일때쯤 오버플로우가 발생함.
계단수란 전,후 숫자 차이가 1 나는 수를 계단수라함!!
*/
extension Array where Element : Comparable{
func sum() -> Int
{
var value = 0
self.forEach
{
value += $0 as! Int
}
return value % 1000000000
}
}
func BOJ_10844()
{
let n = Int(readLine()!)!
var dp = Array(repeating: Array(repeating: 0, count: 10) , count: n+1)
for i in 1...n
{
if i == 1
{
dp[i] = [0,1,1,1,1,1,1,1,1,1]
continue
}
for j in 0..<10
{
if j == 0
{
dp[i][j] += (dp[i-1][j+1]) % 1000000000
}
else if j != 0 && j != 9
{
dp[i][j] += (dp[i-1][j-1] + dp[i-1][j+1]) % 1000000000
}else
{
dp[i][j] += (dp[i-1][j-1]) % 1000000000
}
}
}
print(dp[n].sum())
}
BOJ_10844()
visit my github

'백준 PS일지 > DynamicProgramming' 카테고리의 다른 글
| [백준/Swift] 2096: 내려가기 | PS일지 (0) | 2023.02.09 |
|---|---|
| [백준/Swift] 11048 : 이동하기 문제 뿌수기!! + dp테이블 구하기!! (0) | 2022.08.07 |
| [백준/Swift] 2294 : 동전 2 (0) | 2022.07.19 |
| [백준/Swift] 11052 : 카드 구매하기 (0) | 2022.07.09 |



