https://www.acmicpc.net/problem/11048
11048번: 이동하기
준규는 N×M 크기의 미로에 갇혀있다. 미로는 1×1크기의 방으로 나누어져 있고, 각 방에는 사탕이 놓여져 있다. 미로의 가장 왼쪽 윗 방은 (1, 1)이고, 가장 오른쪽 아랫 방은 (N, M)이다. 준규는
www.acmicpc.net
11048 : 이동하기 / 문제 소개
각 방에는 사탕이 놓여져 있다.
미로의 가장 왼쪽 윗 방(1,1) //준규가 있는 위치
미로의 가장 오른쪽 아랫 방 (N,M) // 준규가 이동해야 할 위치
각 방은 사탕이 있다.
준규는 (r,c)에 있다면, (r+1,c), (r,c+1),(r+1,c+1)로 이동 할 수 있다.
(1,1)에서 (N,M)으로 이동 할 때 가져올 수 있는 사탕 개수의 최대값을 구하시오!
풀이 과정

준규가 (1,1)위치에 있고 (2,2)까지 가는 거리에서 최대 값을 구하는 경우는
준규의 위치에서
오른쪽으로 갔다가 아래,
아래로 갔다가 오른쪽,
대각선
3가지 경우 중 하나 입니다.
답은 1+3+4가 나옵니다.

이 경우 (1,1)에서 (3,2)으로 사탕 최대 개수는?
(1,1)->(2,2)까지 의 최대 경우에서 오른쪽 한칸으로 가는 경우
즉 (2,2까지 사탕 줍는 최대 경우)->(3,2) // 9
(1,2)에서 오른쪽한칸(1,3), 아래(2,3)으로 가는 경우 // 4
(1,2)에서 대각선으로 가는 경우 //13
이 있습니다.
여기서 알 수 있는 사탕의 최대 줍줍 방법은

1,1에서 2,2로 가는 최대 경우는
(1,1)의 최대 사탕 줍는 경우 (1,1) -> (2,2) 대각선으로 가는 경우
(1,2) 최대 사탕 줍는 경우(현재로써는 (1,1) + (1,2)) ->(2,2)로 가는 경우
(2,1) 최대 사탕 줍는 경우( 현재로써는 (1,1)+(2,1)) -> (2,2)로 가는 경우
이 세가지 경우에서 최대값을 구하면 1,1 -> 2,2로 가는 최대 경우를 구할 수 있습니다.
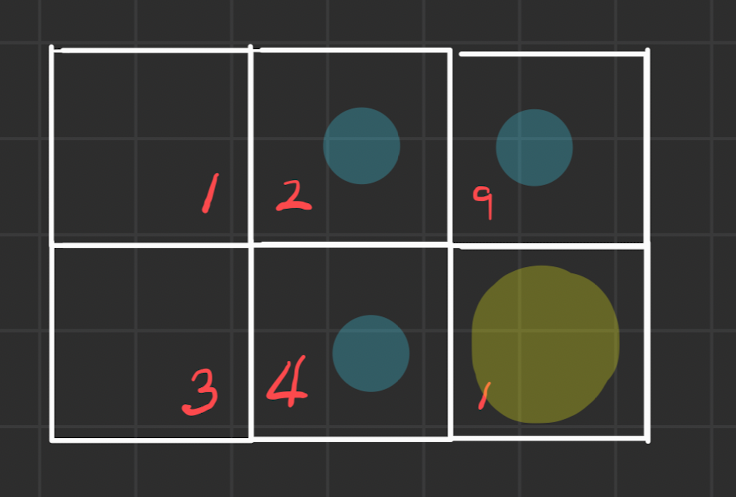
그렇다면 (1,1)에서 (3,2)로 갈 때 사탕 줍줍 최대 경우는??
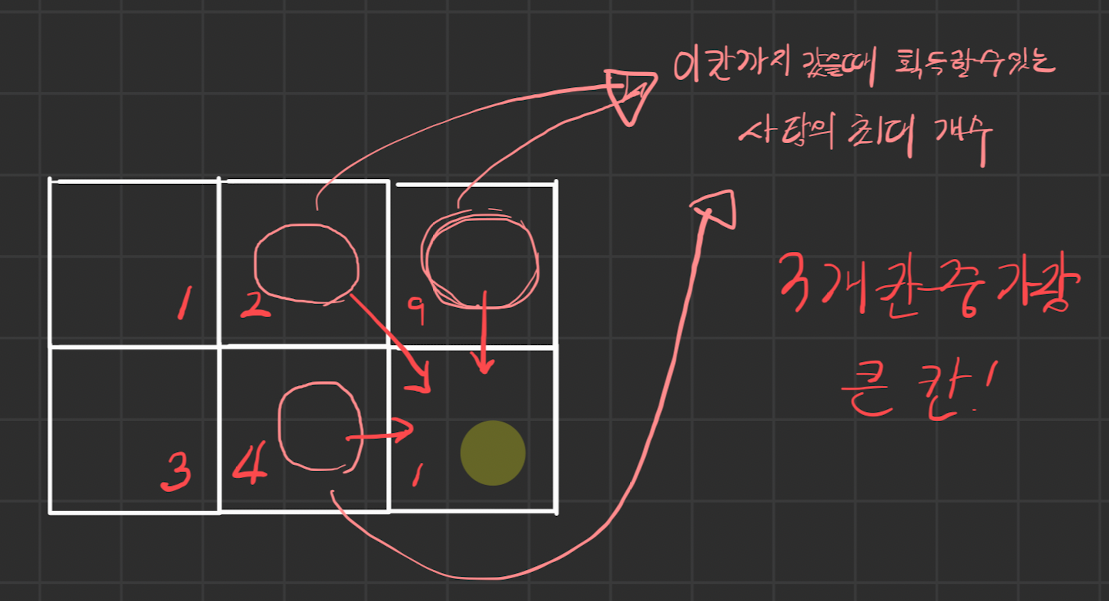
(2,1)에 갔을 때 사탕을 획득할 수 있는 최대 개수 -> (3,1)로 갔다가 -> (3,2)로 가는 경우 // 3+9+1
== (3,1)로 갔을 때 사탕을 획득 할 수 있는 최대 개수 -> (3,2)로 가는 경우
(2,1)에 갔을 때 사탕을 획득 할 수 있는 최대 개수 -> (2,2)로 갔다가 ->(3,2)로 가는 경우 // 3+4+1
== (2,2)로 갔을 때 사탕을 획득 할 수 있는 최대 개수 -> (3,2)로 가는 경우
(2,1)에 갔을 때 사탕을 획득 할 수있는 최대 개수 -> (3,2)로 가는 경우
세 가지 경우 중 한개입니다.
그림으로 그리면
각 칸에 최대한의 사탕을 저장할 수 있는 사탕 개수는 dp 테이블에 저장한다고 가정하고,
공식으로 나타내면
dp[y][x] = max(dp[y-1][x-1],dp[y-1][x],dp[y][x-1]) + x,y일 때 사탕 개수
가 나옵니다.
근데 이 경우에 dp[0][0] 은 max(dp[-1][-1], ... )
바로 에러가 발생합니다. 근데 (1,1)일때도 dp 테이블에 최대 값을 저장 하고 싶은데... (1,2)일 때도 위와 같은 공식을 쓰고 싶은데..
그 해답은 x,y 축에 반 만 zeropadding?! 처럼 0을 씌워주는 것입니다.

호호 이렇게 된다면 (1,1)일때 (2,1)일때 (3,1)일 때 (1,2)일때도 위에 도출한 공식을 통해 사탕의 최대 값을 구해 나갈수 있는 것 입니다!!

dp 배열은 사탕의 배열 가로, 세로에 크기를 1씩 확장한 배열을 만들면 됩니다!
코드 구현
import Foundation
func BOJ_11048()
{
let hw = readLine()!.split(separator:" ").map{Int(String($0))!}
let (height,width) = (hw[0],hw[1])
var rooms = Array(repeating:[Int](), count: height)
for i in 0..<height
{
rooms[i] = readLine()!.split(separator:" ").map{Int(String($0))!}
}
var dp = Array(repeating: Array(repeating: 0, count: width+1), count: height+1)
for y in 1...height
{
for x in 1...width
{
dp[y][x] = max(dp[y-1][x-1] ,dp[y-1][x], dp[y][x-1]) + rooms[y-1][x-1]
}
}
print(dp[height][width])
}
BOJ_11048()
visit my github

'백준 PS일지 > DynamicProgramming' 카테고리의 다른 글
| [백준/Swift] 3067: Coins | PS일지 (0) | 2023.02.16 |
|---|---|
| [백준/Swift] 2096: 내려가기 | PS일지 (0) | 2023.02.09 |
| [백준/Swift] 쉬운 계단 수 문제 풀이 (0) | 2022.07.31 |
| [백준/Swift] 2294 : 동전 2 (0) | 2022.07.19 |



