https://www.acmicpc.net/problem/11727
11727번: 2×n 타일링 2
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다.
www.acmicpc.net
11727 : 2xn 타일링2 / 문제 소개
2*n ( 1<= n <= 1 000 ) 직사각형이 있다.
n은 문제에서 주어진다. 이 직사각형을 1*2 , 2*1 , 2*2 타일로 채우는 방법의 수를 구한다.
이때 n이 커질수록 방법이 많아져 10,007로 나눈다
풀이 과정
규칙을 찾아야 한다... dp는 규칙 찾는게 어려운거 같지만 연습하다보며 늘겠죠..?
- n == 1 인 경우

1*2 크기의 타일 단 한가가 존재한다.
dp[1] = 1
- n == 2 인 경우

이 세가지가 존재한다.
dp[2] = 3
- n == 3 인 경우
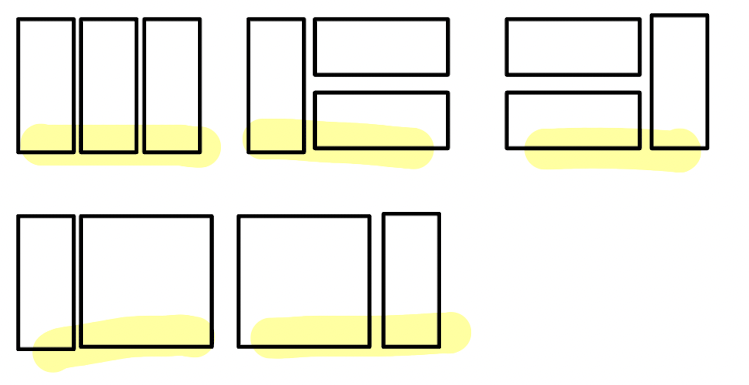
이렇게 다섯가지가 존재한다.
dp[3] == 5
그런데 여기서 이전에 구했던 경우의 수를 활용할 수는 없을까?
맨 왼쪽에 1*2, 2*2 , 2*1 2개를 놓는 방식으로 크게 3가지 경우로 나눠서 구했다.

- 1*2를 놓는 경우 뒤쪽에 위치한 공간은 2*2인데 이 공간에서 가장 많이 놓을 수 있는 타일 경우의 수는 dp[2]에서 구했다.
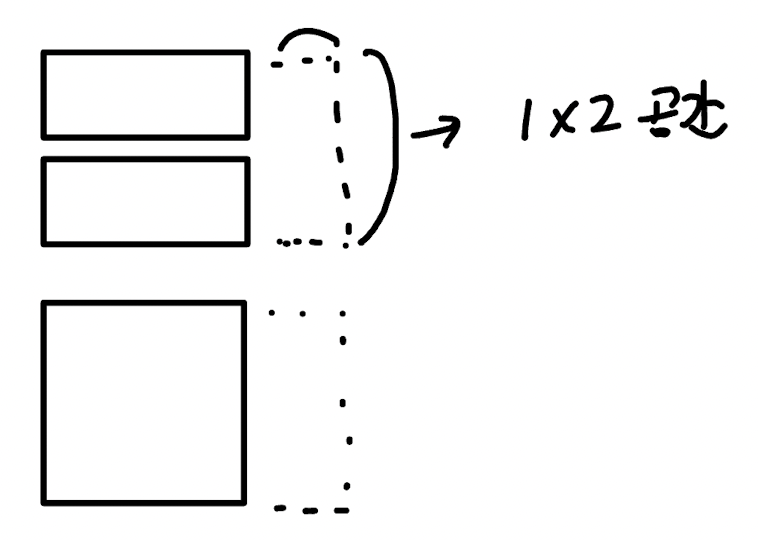
- 2*1 2개 놓는 경우와 2*2 한개 놓는 경우 둘다 1*2의 공간은 1*2 한개밖에 놓지 못하므로 dp[1] 경우의 수가 존재한다
- 2*1 2개와 2*2 1개는 모두 2*2 공간이므로 처음에 2*2 타일을 놓은 후 남은 공간 중 최대 경우의 수 중 *2를 하면 된다.
1 * 2 = dp[2]
2 * 2 = dp[1]
(2 * 1) 2개 = dp[1]
3 + 1 + 1 = 5가 나온다.
- n == 4 인 경우
이 경우도 위에서 구한 패턴을 사용하면 손 쉽게 구할 수 있다.
맨 왼쪽에 1*2 타일 놓는다 가정했을 때
1 * 2타일 = dp[3]
2(2 * 2 타일) = dp[2] *2
5 + 3*2 = 11이 나온다.
n > 2 이상 일때
dp[n] = (dp[n - 1] + 2 * dp[n-2]) % 10007
이렇게 구할 수 있다.
주의할 점은 10007로 꼭 mod 연산을 해야 한다는 것이다.
코드 구현
import Foundation
func BOJ_11727()
{
let n = Int(readLine()!)!
var dp = Array(repeating: 0, count: 1001)
dp[1] = 1
dp[2] = 3
if n > 2
{
for i in 3...n
{
dp[i] = (dp[i-1] + 2*dp[i-2]) % 10007
}
}
print(dp[n])
}
BOJ_11727()
visit my github

'백준 PS일지 > DynamicProgramming' 카테고리의 다른 글
| [백준/Swift] 11052 : 카드 구매하기 (0) | 2022.07.09 |
|---|---|
| [백준/Swift] 2133 : 타일 채우기 문제 완전 뿌수기!! (0) | 2022.07.08 |
| [백준/Swift] 1904 : 01타일 (0) | 2022.07.07 |
| [백준/Swift] 1149 : RGB거리 (0) | 2022.06.25 |



