https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
2133 : 타일 채우기 / 문제 소개
3*N 크기의 벽을 2*1 , 1*2 크기의 타일로 채우는 경우의 수를 구하는 문제입니다.
이 문제도 패턴이 있기 때문에 N이 증가함에 따라 이전에 구한 최대 경우의 수를 반복적으로 필요로 합니다.
풀이 과정
이 문제를 풀어나갈 때 N == 1 , 2 ,3 ,4 ... 30 까지의 경우가 있는데
dp배열 크기 : 31 인 Int형 배열에 n == 1 ~ N 일때 최대 값을 저장해 나갈 것입니다.
dp[1]에는 N == 1일때 최대 경우의 수,
dp[2]에 N == 2일때 최대 경우의 수 ...
이 문제도 규칙이 존재합니다. 그 규칙을 찾는게 정말 중요합니다. ( 규칙찾느라 8장째 N에 대한 타일 채우는 방법을 그렸네요 ㅠ;)
또한 dp 문제이므로 이전에 구한 경우의 수를 활용하는 방법이 중요합니다. 이전에 구한 경우의 수를 최대한으로 활용하는 방법으로
규칙을 찾아 점화식을 형성하는 것이 이 문제의 핵심입니다.
N이 늘어감에 따라 여러 규칙이 존재하는데 이런 규칙 들을 맨 왼쪽에 위치했을때 남은 벽에 대한 경우의 수를 구하면 쉽게 규칙들을 적용할 수 있습니다.
- N == 1 일 때 3 x 1 크기의 벽에 타일을 채우는 경우
이 경우는 존재하지 않습니다.
dp[1] = 0
- N == 2일 때 3 x 2 크기의 벽에 타일을 채우는 경우
이 경우
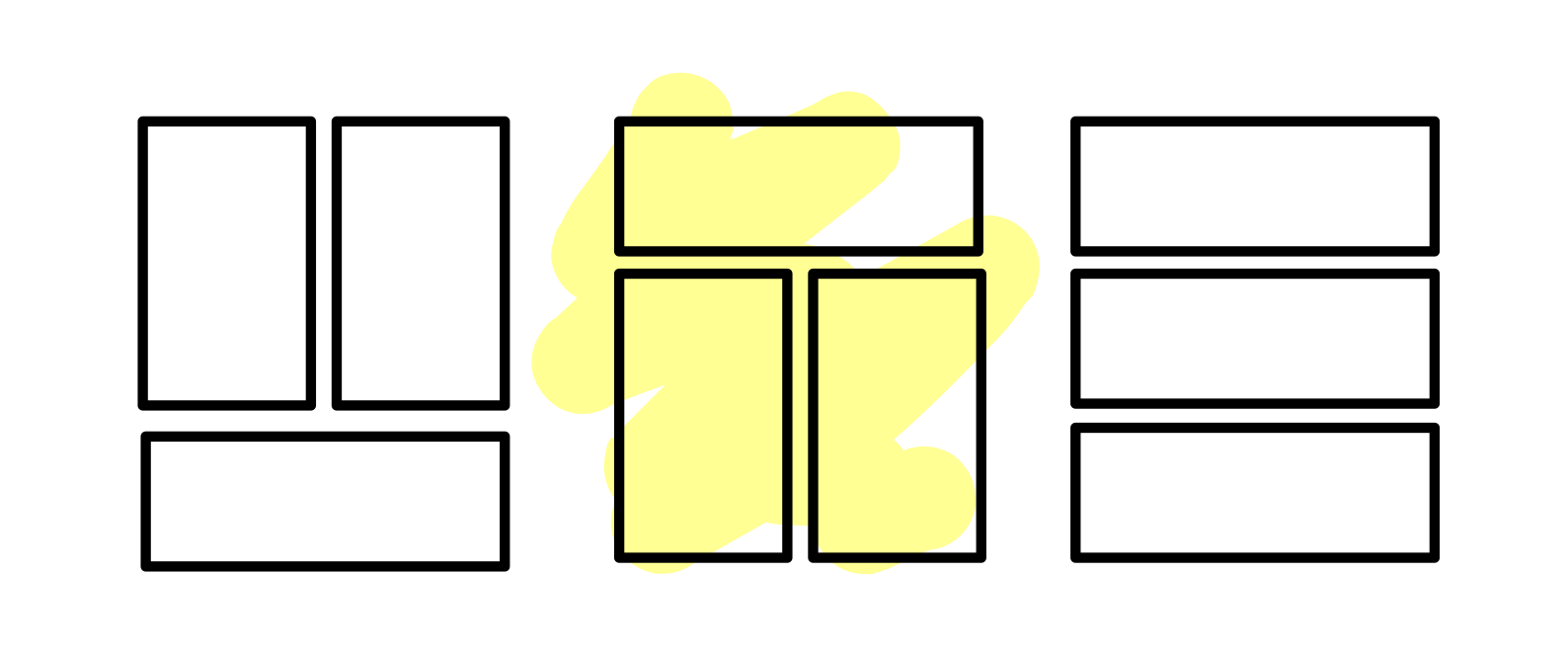
이 세가지의 타일을 놓는 경우가 존재합니다.
dp[2] = 3
- N == 3의 경우 3 x 3 크기의 벽에 타일을 채우는 경우

아무리 다양한 방식으로 타일을 놓아도 1~2 공간이 비게 됩니다. 이럴 경우 3 * 3 타일을 완벽하게 채우는 방법이 존재하지 않아 경우의 수는 0이 됩니다.
dp[3] = 0
- N == 4의 경우 3 x 4 크기의 벽에 타일을 채우는 경우
이 경우를 구할 때 3 x 4크기인 벽은 3 x 2 + 3 x 2의 칸으로 쪼갤 수 있습니다.
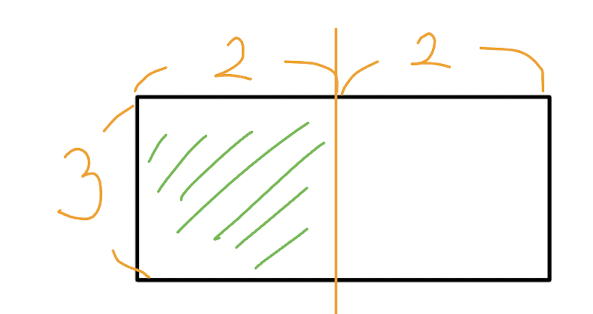
3 x 2의 칸은 dp[2] . N == 2일 때 구했던 최대 경우의 수인 3이 존재합니다. 더 높은 값이 나올 수 없습니다.
왼쪽에 칠한 3 x 2 벽에서 최대 타일 놓는 경우의 수 dp[2] 동시에 오른쪽 흰색 3 x 2칸에 놓을 수 있는 타일 최대 수 dp[2].
dp[4] = d[2] * d[2] 를 통해 구할 수 있습니다.
잠깐!! 이 외에도 타일을 놓는 다른 방법은?? 존재합니다..... 이 문제의 핵심 포인트입니다.

(좌)이렇게 놓는게 아니라 (우) 형태로 놓는. 새로운 유형의 타일 놓는 형태입니다.

(좌)이렇게 가운데 3 x 2의 형태로 자를 수 없으며 (1 x 1 타일 없음).
(우) 좌측 3 x 1형태로 자를 수 없습니다.
이 경우 2 x 1 타일이 아래 말고 위에 올라가는 경우

이렇게 두가지 경우가 존재합니다. 저는 이제부터 이런 패턴을 주황색 색칠된 패턴으로 부르겠습니다. 이 경우는 이전에 구했던 N == 2일때 최대 경우의 수 dp[2]를 이용할 수없습니다.
잘라도 1x1 타일이 없기 때문..
따라서 이 두 경우의 를 더하면
dp[4] = dp[2] * dp[2] + 2
- N == 5의 경우
이 경우는 여러번 타일을 놓아보시면 알겠지만 빈 공간이 생기게 됩니다.
N이 홀수 인 경우 타일을 전부 채울 수 없기에 홀수는 경우의 수 가 전부 0입니다.
이제부터 짝수만 경우의 수를 찾겠습니다.
- N == 6의 경우 3 x 6의 벽에 타일을 놓는 경우의 수
이 경우에도 이전에 구했던 최대 경우의 수를 반드시 활용해야 합니다.
우선 이전에 구한 패턴들은 dp[2] , dp[4] 그리고 dp[4]일때 주황색 색칠된 패턴 2개가 있습니다.
3 x 6은 3 x 2와 3 x 4로 잘라 이전에 구했던 dp[2] dp[4]를 활용하는 방법이 있습니다.
3 * 6의 공간에서 3 *2의 공간을 자른 경우( == 일단 dp[2]를 맨 왼쪽에 놓는 경우)
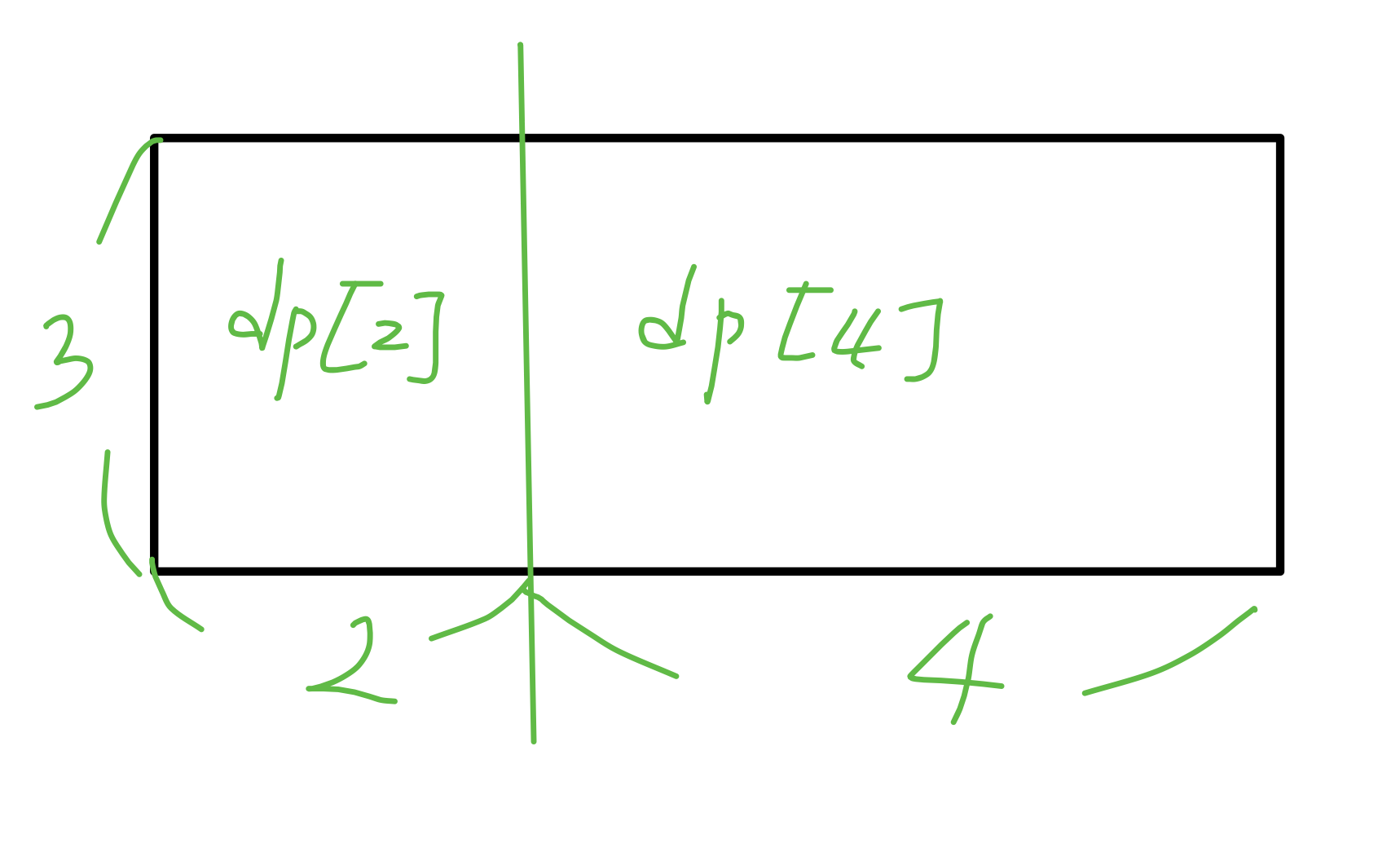
3 * 2 의 공간에서는 dp[2]가 최대 경우의 수 이므로, 남은 공간 3*4 에 대해서는 이전에 구한 dp[4]가 최대 경우의 수입니다. 이 dp[4]에는 색칠된 주황 패턴도 포함되어있으므로 최대 경우의 수가 됩니다.
dp[6] = dp[2] * d[4]
맨 왼쪽에서 3 * 4의 공간으로 자른 경우를 살펴보면
이미 dp[2] * dp[4]에서 dp[4]의 경우를 보면 dp[2]*dp[2] + 2인데 2(색칠된 주황 패턴은 제외하고)
d[2] * dp[2] * dp[2] 의 경우가 이미 존재합니다.
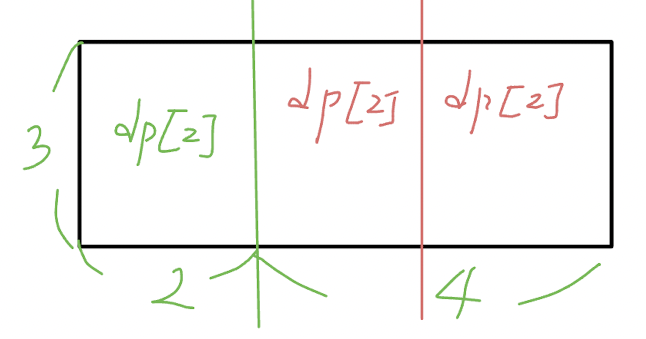
이렇기 때문에 3*4일때 dp[4]의 경우는 중복된 경우의 수 dp[2] * dp[2]가 존재하기 때문에 dp[4]는 활용할 수 없습니다.
남은건 dp[4]일때 주황색으로 색칠된 패턴 2개가 존재합니다.
이 경우를 맨 왼쪽에 놓을 수있습니다.
이전에 구한 dp[2] * dp[4]의 경우 주황색으로 색칠된 패턴 2개가 우측에만 적용됬기에
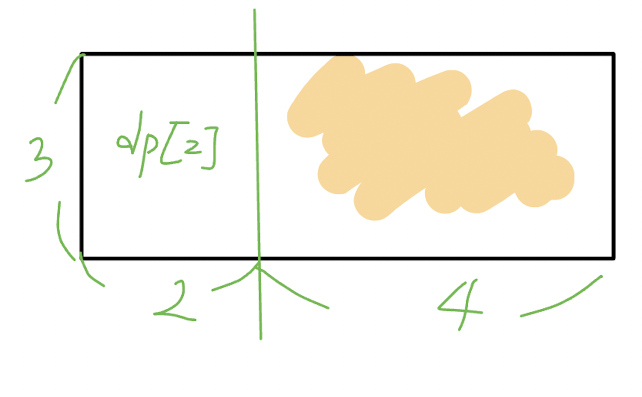
왼쪽일 때도 적용이 되어야 합니다.
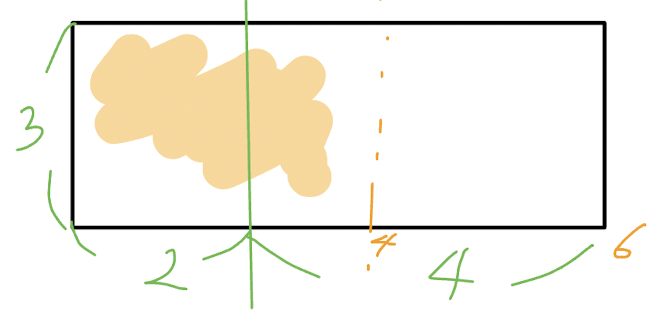
이 색칠된 주황 패턴 2개가 놓였을 경우 남은 공간은 3 * 2의 벽인데 이때 타일을 놓을 수 있는 최대 경우의 수는 dp[2]입니다.
따라서
dp[6] = (색칠된 주황패턴 왼쪽에 올 때)2 * dp[2]
를 구할 수있습니다.
이게 끝인가요? 아닙니다!!!!!!!
dp[4]일때 구한 주황색으로 색칠된 2개의 패턴은 좀 특이했었는데 3*6일때도 역시 N== 4의 색칠된 주황 패턴과 유사하게 독보적인 2개 패턴이 존재하는 것입니다.
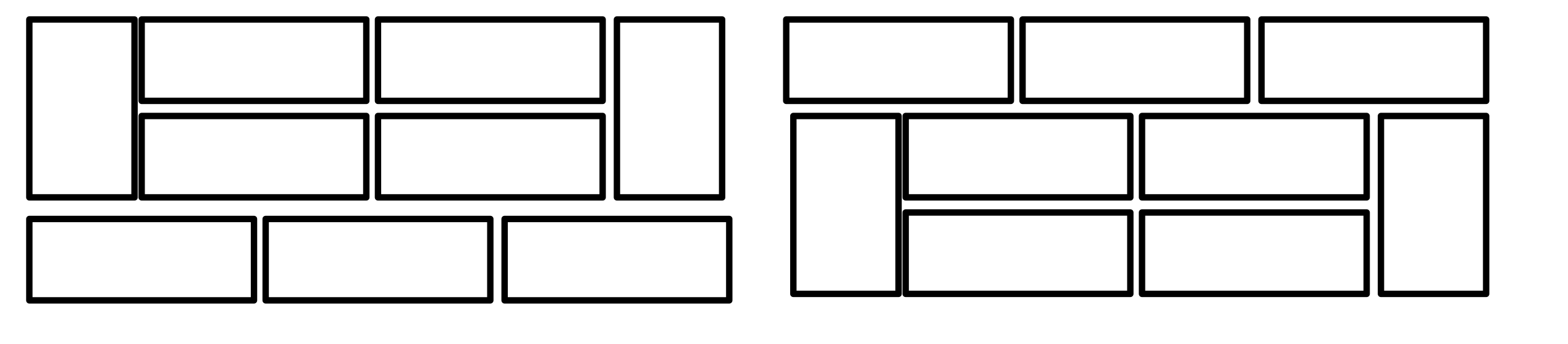
3 x 2( dp[2]를 구했기에,,) 나 3 x 4(dp[4]를 활용 할 수 있는) 의 크기로 자를 수 없습니다. 1*1 타일이 존재하지 않으니까요
이번엔 이 두 패턴을 역시 6칸으로 색칠된 주황 패턴으로 부르겠습니다.
결국 dp[6]은
dp[6] = dp[2] * dp[4] + (색칠된 주황패턴 N==4일때) 2 * dp[2] + (색칠된 주황 패턴 N == 6일때)2
의 합으로 최대 경우의 수가 dp[6]에 저장됩니다...
dp[6] = dp[2] * dp[4] + 2 * dp[2] + 2
이쯤이면 패턴을 찾은 분도 있겠지만 혹시 모르니 N == 8일때도 구해보겠습니다.
- N == 8의 경우 3 x 8의 벽에 타일을 놓을 수 있는 경우의 수
3 x 8은 우선 3 x 2와 3 x 4와 3 x 6 으로 잘라 각각의 경우 dp[2] dp[4] dp[6]을 활용한 최대 경우의 수를 구할 수 있습니다.
1. 맨 왼쪽을 3 x 2로 자른 경우 ( 3x 2 + 3x 6)
이 경우는 dp[2] * dp[6]의 형태가 됩니다.
2. 맨 왼쪽을 3 x 4로 자른 경우 (3 x 4 + 3 x 4)
이 경우는 아까 dp[6]에서 경우와 마찬가지이지만 한번 더 설명을 하자면
맨 왼쪽을 3 x 2로 잘랐을 때dp[2] * ( dp[6]안에 ) dp[2] *dp[2] * dp[2] 이 경우의 수가 존재합니다.
이제 맨 왼쪽을 3 x 4로 잘랐을 때 dp[4] * dp[4]는 각각 (dp[2] * dp[2] + 2) * (dp[2] * dp[2] + 2)이기 때문에 역시나
dp[2] * dp[2] * dp[2] * dp[2] 인 경우의 수가 존재합니다. dp[2]*dp[6]일때 이미 구한 것이므로 dp[4]는 사용할 수 없습니다.
그렇다면 3 x 4는 못쓰는가? nono
3 x 4일때 구한 주황 패턴은 사용할 수 있습니다.
" 아니 이미 그 주황패턴은 3x 6일때 사용한거 아니에요?"

그건 dp[6]일때 우측에 한에서만 구한거여서.. 아직 맨 왼쪽을 3*4로 나눴을 때
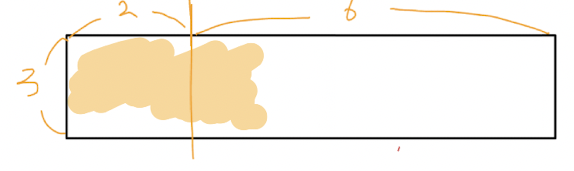
색칠된 주황 패턴을 적용시킬 때도 이전에 구한 dp[2]*dp[6] 과 중첩되지 않으면서도 경우의 수를 구할 수 있어요!!
색칠된 주황 패턴(N == 4)는 2개존재하고, 나머지 빈 3 * 4 공간에 대해서는 dp[4]가 최대 경우의 수 이므로
dp[8] = 2 * dp[4]
를 적용시킬 수 있습니다.
이번엔 3 x 6으로 맨 왼쪽을 잘르고 3 x 2가 남은 경우도 보면
3 x 6일때 최대 경우의 수는 dp[6] 그때 남은 오른쪽 공간(3*2)에 대해서 dp[2]를 통해 dp[6] * dp[2]를 구할 수 있지만 이는 아까
N ==8을 구할때 dp[2] * dp[6]의 경우의 수와 dp[2]*dp[2]*dp[2]*dp[2]와 위에서 구한 색칠된 주황패턴(n==4)일때 가 겹치므로 사용할 수없습니다.
그럼 3x6일때는 사용을 아예 못하냐? 또 경우의 수가 있습니다.

맨 왼쪽을 3 x 6으로 잘랐을 때 dp[6]은 불가능하지만 N==6일때 색칠된 주황 패턴(우측과 같이)을 적용시켜야 합니다.
dp[8] = 2 * dp[2]
를 구할 수있습니다.
여태까지 구한걸 총 합쳐보면
dp[8] = dp[2] * dp[6] + 2*dp[4] + 2*dp[2]
휴 여기서 끝인가?
아닙니다. N==4 와 N==6일때 존재했던 색칠된 주황색 패턴이 N==8일때도 존재합니다.;;

네.. 이것도 마찬가지로 3x2나 3x3, 3x4,3x5 등으로 자를수도 없는 독보적인 색칠된 주황패턴..2개입니다.
따라서
dp[8] = dp[2] * dp[6] + 2*dp[4] + 2*dp[2] + 2
지금까지 구해온 dp를 확인해보면
dp[2] = 3
dp[4] = dp[2] * dp[2] + 2
dp[6] = dp[2] * dp[4] + 2 * dp[2] + 2
dp[8] = dp[2] * dp[6] + 2*dp[4] + 2*dp[2] + 2
점화식을 구하자면..
dp[n] = dp[2] * dp[n-2] + 2(dp[n-4] + dp[n-2] + ... + dp[2] + 1)
을 구할 수 있습니다.
이때 맨 오른쪽 1은 dp[0]에 저장해 주면 포문을 돌릴 때 편하겠죠? 아니면 뭐 포문이후에 1을 추가로 더 해줘도 되지만 포문사용을 편안하게 하기 위해 dp[0] = 0 이지만 dp[0] = 1 을 대입해서 구할 것입니다.
코드 구현
import Foundation
/**
* 이 문제 풀면서 변수는.....
* n==4이면
* 원래 2칸씩 나눠서 dp[2]가 아닌 새로운 2개의 디자인과
*
* n==6 이면
* 원래 4칸일때 있었던 신기한.. 반으로 쪼갤 수없는 2개의 디자인 + 6개일때 또한 2개씩 3번 나눌수 없는
* 유일한 디자인 한개 * 상하 바뀐게 존재한다는거다.
*
* n == 8이면
* 원래 4일때 신기 + 6일때 신기 + 8일때 연속적인 디자인으로인해 2칸씩 쪼갤 수 없는 새로운 디자인이 2개 생긴다는 것이다ㅏ..
* 의 반복이다.
*/
func BOJ_2133()
{
var n = Int(readLine()!)!
var dp = Array(repeating: 0, count: 31)
dp[0] = 1
dp[2] = 3
for i in stride(from: 4, through: 30, by: 2)
{
dp[i] = dp[2]*dp[i-2]
for j in stride(from: i - 4, through: 0, by: -2)
{
dp[i] += 2*dp[j]
}
}
print(dp[n])
}
BOJ_2133()
긴 글 읽어주셔서 감사합니다.
visit my github

'백준 PS일지 > DynamicProgramming' 카테고리의 다른 글
| [백준/Swift] 2294 : 동전 2 (0) | 2022.07.19 |
|---|---|
| [백준/Swift] 11052 : 카드 구매하기 (0) | 2022.07.09 |
| [백준/Swift] 1904 : 01타일 (0) | 2022.07.07 |
| [백준/Swift] 11727 : 2×n 타일링 2 (0) | 2022.07.07 |



