
라이노님 힙 상세 리뷰(안 까먹기 위해..) + 최소 힙 개념 정리
라이노님 힙 구조
struct Heap<T> where T: Comparable {
private var heap = [T]()
let compare: (T,T) -> Bool
var isEmpty: Bool { return heap.isEmpty }
init(compare: @escaping (T,T) -> Bool) {
self.compare = compare
}
init() {
self.init(compare: <)
}
}다익스트라에선 최소 힙을 주로 사용합니다. 루트 노드로 갈 수록, value가 작아야 한다는 특징이 있습니다. heapify 성질을 만족 시켜야 합니다. compare 클로저는 두 T generic type의 두 원소에 대해서 Comparable을 통해 비교 후 Bool 값을 반환합니다. 이때 기본적으로 compare: <로 했습니다. 이 경우 왼쪽이 오른쪽보다 작을 때 true를 반환합니다.
Heap 삽입 연산
extension Heap {
mutating func insert(_ element: T) {
var idx = heap.count
heap.append(element)
while idx > 0 && compare(heap[idx], heap[(idx-1)/2]) {
heap.swapAt((idx-1)/2, idx)
idx = (idx-1)/2
}
}
}최소 heap을 삽입할 때 사용하는 함수입니다.
Heap 삽입 예
[10, 5, 8, 3, 9] 최소 힙에 삽입할 때의 과정입니다.
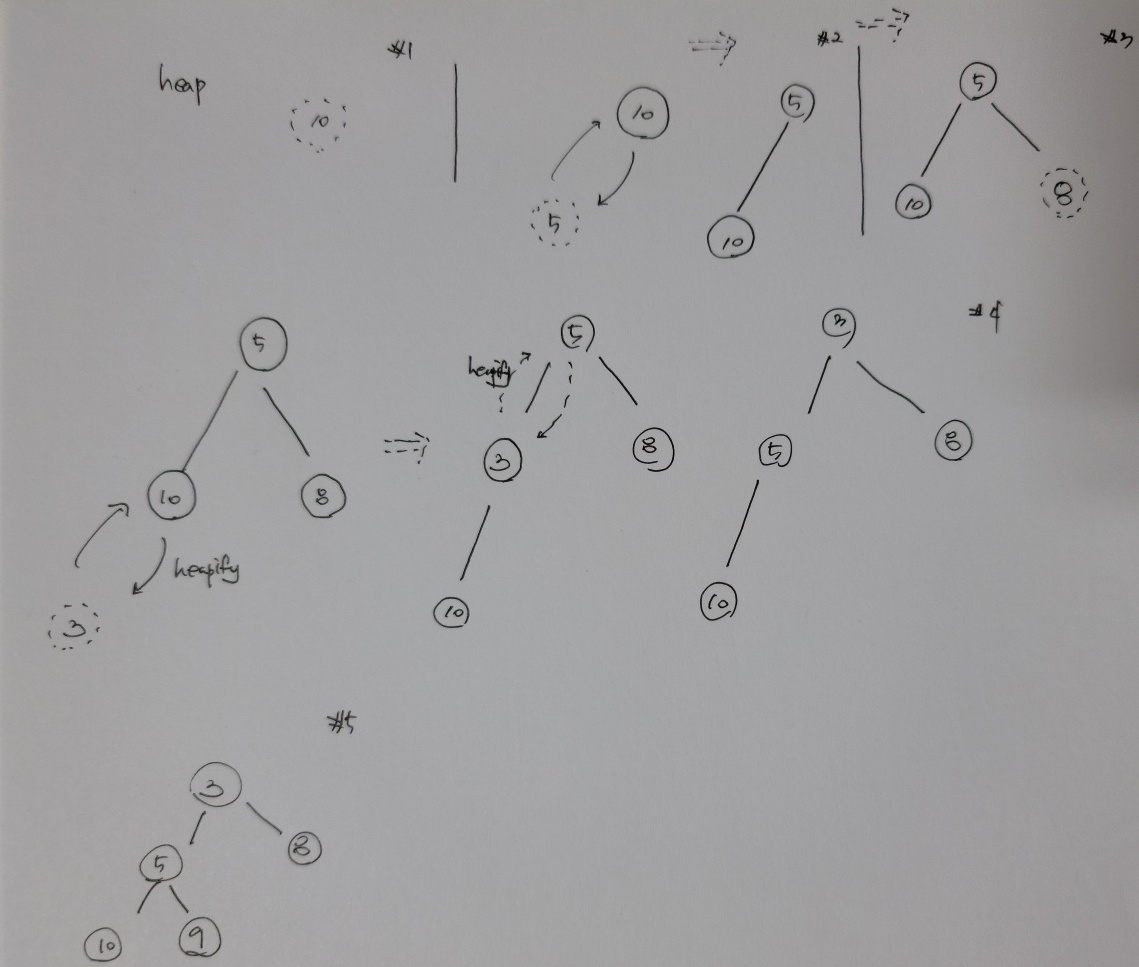
코드에선 heap의 0번째 index부터 원소를 배열의 맨 뒤에 append한 이후 자신의 parent node와 heapify 성질을 비교해서 heapify 성질을 만족할 때까지 비교를 합니다. root node index == 0이기 때문에 특정 node의 index에서 parent node를 구하기 위해선 index-1을 한 후에 /2를 해야합니다.
코드에서 idx는 최근에 추가된 element입니다.(heapify 성질 만족 했는지 체크해야 합니다.) 주의깊게 봐야할 것은 comapre입니다. compare은 {$0 < $1 } 일때 true를 반환합니다. 그림에서 보듯 하위노드가 자신의 부모노드보다 작을 경우에만 while문이 동작합니다.
위 그림에서 '3'을 넣을 때 과정을 보면
10 // (( idx-1 ) /2)
3 // idx
compare가 true 되야 합니다. 근데 compare는 {$0 < $1}일때 $0이 작을 때만 while문이 지속적으로 동작합니다. 따라서 10 < 3 의경우는 안되고 3 < 10 이 되도록 compare(idx, (idx-1)/2)가 되야합니다. ( 엇,, 근데 왜 while문의 comapre((idx-1/2),idx)가 도 되는거죠?...;;)
Heap 삭제 연산
extension Heap {
mutating func delete() -> T? {
guard !heap.isEmpty else {
return nil
}
guard heap.count != 1 else {
return heap.removeFirst()
}
let res = heap.first!
heap.swapAt(0, heap.count-1)
_ = heap.removeLast()
var idx = 0
while idx < heap.count {
let (left,right) = (idx*2+1,idx*2+2)
if right < heap.count { //#1
if compare(heap[left], heap[right]) && compare(heap[left], heap[idx]) { //#2
heap.swapAt(left, idx)
idx = left
}else if compare(heap[right],heap[idx]) { //#3
heap.swapAt(right, idx)
idx = right
}else { //#4
break
}
}else if left < heap.count { //#5
if compare(heap[left], heap[idx]) { //#6
heap.swapAt(left, idx)
idx = left
}else { //#7
break
}
}else { //#8
break
}
}
return res
}
}Heap 삭제 예

삭제연산은 무조건 루트노드의 원소가 pop됩니다. 이때 heapify 성질을 쉽게 유지하기 위해 루트노드와 배열의 맨 마지막 원소의 자리를 바꾼 후에 맨 마지막 원소는 루트노드가 되었음으로 pop시킵니다.
이후 변경된 루트노드는 heapify를 만족하도록 left or right. 하위 노드로 내려 가면서 heapify를 만족할 때까지 자식노드와 비교 후 내려가야합니다.
이때 크게 3가지의 경우가 있습니다.
1. 비교 대상 노드의 자식 노드가 두 개 있을 경우 ( if right < heap.count )
- left, right 중 어느 자식이 작은지 반드시 판별해야 합니다. 그 후 교환을 할 경우 신기하게 노드가 한쪽으로 쏠리지 않고 heapify성질을 만족하게 됩니다.
- 루트노드에서 부터 heapify성질을 만족하는 위치에 자리하기 까지 거의 대부분 이 과정을 거칩니다.
2. 비교 대상 노드의 자식 노드가 한 개 있을 경우 (if left < heap.count )
- 이 경우 단순하게 왼쪽 자식 노드가 parent 노드보다 value가 큰지 작은지만 판단 하고 끝내면 됩니다.
- 비교 대상 노드의 left 자식 노드는 리프 노드입니다.
- 비교 대상 노드가 리프 노드(더 이상 자식이 없는 경우) 입니다.
그림1을 보시면 6은 heapify성질을 만족하지 않습니다. 자식 노드보다 값이 크기 때문입니다. heapify 성질을 만족하기 위해선 자식 노드 중 한 노드와 바꿔야 합니다. 5가 적합할 까요 9가 적합할 까요. 5가 적합하겠죠? 그래서 일단 비교 대상 노드(6)의 두 자식 노드(5,9)간에 가장 작은 노드의 위치를 확인해서 그 위치에 넣어야 합니다.
중요한 것은 상위 노드보다 하위노드 중 하나라도 heapify 성질을 만족하지 않는 원소가 있다면 바꿔야하는게 힙의 특징입니다. 또한 left, right 중 작은 자식 노드를 찾는게 핵심입니다.
- 1. 비교 대상 노드의 자식 노드가 두개 있는 경우 // 1
// parent의 자식노드가 두개 있으면서 left가 right보다 작고 parent보다 작을 때
if compare(heap[left], heap[right]) && compare(heap[left], heap[idx]) { //#2
heap.swapAt(left, idx)
idx = left
}
#2 부분에서 아래의 예를 적용해 보겠습니다.
(참고로 아래의 6은 특정 노드. 5와 9는 6의 child node 입니다.)
6 //idx
5 //left 9 //right
여기선 5가 나와야합니다. #2의 조건문에서 heap[left] 는 heap[right]보다 작다. (true). heap[left] < heap[idx] true 이 경우엔 왼쪽이 오른쪽보다 작으면서도 상위 노드보다 작기 때문에 idx과 left의 위치를 바꿔야 합니다.
//parent의 자식 노드가 두 개 있고 right가 left보다 작고 parent 노드보다 작을 때
else if compare(heap[right],heap[idx]) { // #3
heap.swapAt(right, idx)
idx = right
}이 경우는 left가 right보다 클 경우에 해당됩니다. right는 자신의 부모 노드보다 작을 경우 heapify성질을 위반함으로 부모노드와 자리를 바꿔야합니다. 그 예로
6 //idx
9 // left 5 // right
이 경우가 있습니다. 다시 #2 조건에서 이 예제를 적용해 보면
if compare(heap[left],heap[right]) && ...
{9 left < 5 right } left가 작지 않기 때문에 #2의 if구문은 실패입니다. 즉 left가 제일 작지 않다는 것입니다.
#3을 적용해 본다면 compare(5, 6) 작기 때문에 교환해야합니다!!
else { //#4
break
}#4의 경우는 두 자식이 parent보다 큰 경우 입니다.
6 //idx
9//left 7//right
이 경우가 있습니다.
대부분은 #1의 조건문이 실행 됩니다.
#5의 경우 left는 리프노드입니다. ( 마지막 전 while문 )
else if left < heap.count { //#5
if compare(heap[left], heap[idx]) { //#6
heap.swapAt(left, idx)
idx = left
}else { //#7
break
}#5. 이 경우 child node가 1개인 경우 입니다. 우선순위 큐를 구현하는 최소 힙, 최대힙의 heapify는 완전 이진 트리를 만족해 나가야 합니다. 따라서 자식이 한 개다. == left밖에 없다! 왜냐면 배열의 마지막 인덱스에 element가 차곡 차곡 쌓이기 때문입니다. + heapify성질을 만족시키는 코드를 실행해서.
6 //idx
5 //left
#6 이 경우 compare(5, 6)입니다. parent는 자식보다 커야하는데 자식이 작기 때문에 heapify 위반입니다. 따라서 둘의 자리가 swap되어야 합니다.
6 //idx
7// left
이 경우 #6의 조건은 실행되지 않습니다. 자식이 부모보다 더 크기 때문입니다. 그렇다면 성공적으로 heapify성질을 만족하게 된 것임으로 while문을 빠져나오는 #7이 실행됩니다.
----
case 1
6 //idx
4 7
->
4
6 //idx 7
더이상 자식 x
-----
case 2
7 //idx
6
->
6
7// idx
더이상 자식 x
#8입니다. case 1 또는 case2를 통해 parent보다 작은 자식이 있어서 swap을 한 이후 에 더 이상 자식이 없는 경우에 해당됩니다.
다익스트라 알고리즘을 공부하면서 라이노님의 Heap<T>를 보지 않으며 혼자 만들었는데 특정 compare의 left, right or idx위치가 정확하게 들어가지 않아도 코드가 실행되긴 하는데 실행시간이 많이 느려진다는 것을 알았습니다!! 원조가 최고긴 한데,, 안 보고 만들다 보니 신기한 경험을 했다고 생각합니다.
내용 중 틀린 부분이 있을 수 있습니다. 알려주신다면 감사합니다.
'ComputerScience > Algorithm concepts' 카테고리의 다른 글
| [Algorithm/Swift] 문자열 탐색. KMP 알고리즘 파해치기!! 부분 일치 테이블 pi 채우는 방법 (4) | 2023.01.27 |
|---|---|
| [Algorithm] 플로이드 와셜(Floyd-Warshall) 개념 뿌수기!! (0) | 2023.01.10 |
| [Algorithm] 그래프의 의미 및 DFS, BFS 탐색 방법 기본 개념 완전 뿌수기!!!! (0) | 2022.09.16 |
| [알고리즘]다익스트라 최단 경로 알고리즘 개념 부수기 / heap이 뭐야? (0) | 2022.08.27 |



