
요즘 문자열 알고리즘을 공부하고 있습니다. 문자열 탐색에 많이 사용되는 kmp 알고리즘에 대해서 공부한 개념을 정리하려고 합니다.
ctrl + f를 통해 trans라는 단어를 찾아봤습니다.
주어진 text에서 "trans"라는 pattern을 찾았습니다. 문자열 탐색이란 주어진 text에서 특정한 단어 pattern을 찾는 것을 의미합니다.
Knuth, Morris, Pratt 세 사람이 만든 KMP 알고리즘이 문자열 탐색에 유명합니다. 그 전에 먼저 문자열 탐색의 가창 기초적인 방법을 설명한 후에 kmp 알고리즘을 통한 문자열 탐색 알고리즘을 소개하려고 합니다.
1. 기본적인 문자열 탐색 방법 Naive string search
주어진 문장에서 특정한 문자열을 찾을 수 있는 방법이 뭐가 있을까요?
주어진 문장을 text라고 하고 내가 찾고자 하는 특정한 문자열을 pattern이라고 하겠습니다. 주어진 text에서 특정 pattern문자를 찾는 방법은 text를 가장 왼쪽에서부터 오른쪽으로 훑어가면서 동시에 text의 글자와 pattern의 첫 글차가 일치하는가 입니다. 만약 text의 특정 위치 i가 pattern의 첫 위치와 일치한다면 pattern의 두번째 문자와 text i+1의 문자를 비교해가면서 pattern의 마지막 길이까지 문자를 비교해 나갈 것입니다. i + a(a<pattern.size()) 위치에 text와 pattern의 문자가 다르다면 해당 문자열은 pattern이 아님으로 원래 첫 문자를 비교했던 index i에서 그 다음칸 문자를 pattern의 첫 문자와 비교하면서 문자열을 탐색해 나갑니다.
text: "aba abb abababa"
pattern: "abab"
text의 맨 왼쪽 문자의 index == 0이라고 하겠습니다.
// 중요한 것은 index는 text의 위치를 가리킵니다.
1. text의 index 0부터 pattern 의 첫 문자와 일치하는지?
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| text | a | b | a | a | b | b | |||
| pattern | a | b | a | b | |||||
일치한다면 그 다음 문자도 일치하는지의 여부를 봅니다. text의 idx 3이 일치하지 않습니다. 패스!
2. text의 index +1증가해 pattern의 첫 문자와 같은지 비교
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| text | a | b | a | a | b | b | |||
| pattern | a | ||||||||
x
3. text의 index 2와 pattern a 비교, 일치한다면 다음 문자 비교
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| text | a | b | a | a | b | b | |||
| pattern | a | b | |||||||
x
...
4. index의 8번째가 text에서 pattern과 일치하네요.
| Index | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| text | a | b | a | b | a | b | a | ||
| pattern | a | b | a | b | |||||
5. index 10일 때도 pattern 과 같습니다.
| Index | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| text | a | b | a | b | a | b | a | ||
| pattern | a | b | a | b | |||||
index 8, 10에서 두 개의 pattern 문자열을 찾을 수 있습니다.
즉 text를 0번째 index부터 11번째 index까지 (text.size - pattern.size) 루프 탐색을 해야 합니다.
text의 각각의 index에 대해서 pattern.size만큼의 루프 탐색을 해야 합니다.
func naivePatternSearch(text: [String], pattern: [String]) {
let (n,m) = (text.count,pattern.count)
for i in 0..<(n-m+1) {
for j in 0..<m {
if text[i+j] != pattern[j]{
break
}
if j==(m-1) {
print("Pattern found: \(i) index"
}
}
}
}시간복잡도는
겉 for 루프 n - m - 1
안 포문은 m
즉 O(nm) 입니다.
// index는 text의 위치를 가리킵니다.
단점이 있을까요?
| Index | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| text | a | b | a | b | a | b | a | ||
| pattern | a | b | a | b | |||||
index 8일 때 text의 8,9,10,11이 pattern abab와 일치한다는 것을 알았습니다.
그리고 pattern을 자세히 보면 ab ab 가 반복된 형태입니다. 여기서 알 수 있는 내용: "9번째는 무조건 안되는구나"를 알 수 있습니다.
b
a
text의 10번째 index부터 11번째 index까지 무조건 pattern과 같은 단어구나!!
text의 index 8번째 위치에서 9,10,11까지 4개의 문자를 비교했고 index 10에서 시작한다면 12, 13이 같은지만 비교할 수 있을텐데..
9번째부터 다시 4개의 text와 pattern간 단어가 같은지 확인해야 한다는 점이 있습니다. 이게 바로 단점입니다.
접두사와 접미사가 일치한 pattern의 특정 위치를 구했다면 해당 내용을 이용하면 좋은데 그럼에도 처음부터 다시 구해간다는 것입니다.
접두사와 접미사? 아래에서 다룹니다!
kmp algorithm은 text index i위치에서 부터 i+pattern.count-1까지!! 이전에 구했던 정보를 바탕으로 접두사와 접미사가 같다면 이전에 구한 특정 위치로 건너뛴 후 이전에 일치했다는 것을 이용하면서 새로운 text의 위치에서 pattern과 비교를 시작합니다.
2. KMP Algorithm
kmp 알고리즘을 공부하기 전에 알아야 할 개념이 있습니다.
접두사(prefix)와 접미사(suffix)의 개념, 이전에 구한 정보를 저장하는 pi배열입니다.
apple 단어에서 접두사prefix는
a, ap, app, appl, apple 이 됩니다.
접미사suffix는
e
le
ple
pple
apple
이 됩니다.
이제 KMP 알고리즘의 개념에 대해 소개합니다. 아래에는 한가지 예시가 있습니다!
// index는 text의 위치를 가리킵니다.
| Index | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| text | a | b | c | d | a | b | c | d | ? | |
| pattern | a | b | c | d | a | b | c | w | ||
text문자열의 7번째 index를 보시면
text 문자열: ...?abcdabcd?.... // 중요한 것은 index 7부터 pattern과 비교를 한다는 것. idx 6 == ?, i+pattern.size == ?로 표시.
pattern 문자열: abcdabcw입니다.
여기서 14번째 index가 같지 않기 때문에 아무리 pattern에서 index 0...6까지가 일치했다 하더라도 index 7 부터 시작되는 pattern 단어와 text 단어는 일치하지 않습니다.
"아하.. index7은 pattern과 일치하지 않구나."
그렇다면 다음으로 해야할 일은 시작 위치를 찾는 방법입니다. 시작 위치를 찾고 pattern의 첫 문자부터 차례대로 비교해 나가기 위함입니다. index7부터 시작했지만 pattern과 불일치가 발생했습니다. 어떻게 다음 시작 위치를 찾을 수 있을까요?
브루트 포스적인,, naive 방식을 사용한다면 7번째 index에선 pattern를 찾지 못했음으로 index +1을 해서 pattern의 문자를 비교해 나갈 것입니다. 가장 좋은 방법은 무엇일까요?
index 7 다음의 문자열 중 a로 시작하는 문자의 위치 정보를 찾는다?
or 14번부터 pattern 비교? or 15번부터 패턴 비교??
14, 15번부터 패턴의 첫 문자를 비교하게 될 경우 정확한 답이 나오지 않습니다. index 7 이후의 문자열 중 a로 시작하는 문자를 찾을 수 있습니다. 하지만 이보다 훨씬 좋은 방법은 text index 7일때 이미 7, 8, 9, 10, 11, 12, 13번째 까지 비교했고 14번째 index 마지막 문자는 틀렸지만 그 이전까지의 문자들은 일치했음을 이용하는 것입니다. 방금 비교한 7글자 중에서 새로운 시작 위치를 찾는게 가장 좋은 방법입니다.
즉 i번째에서 시작한 문자열 매칭이 불일치 할 때, i 다음으로 탐색해야 할 대상은 어느 것으로 선정해야 가장 최적화 된 next start 값 인지를 고민해야 합니다. kmp 알고리즘은 i번째 일때 매칭됬던 substring(index 7 ... 13)을 버리지 않고 i의 다음으로 탐색 시작할 index를 정하는 방법입니다.

한 눈으로 봐도 딱 나옵니다. 빨간색으로 체크된 a위치 입니다. 어떻게 구할 수 있었을까요?
패턴 불일치 문자 w는 제외합니다.
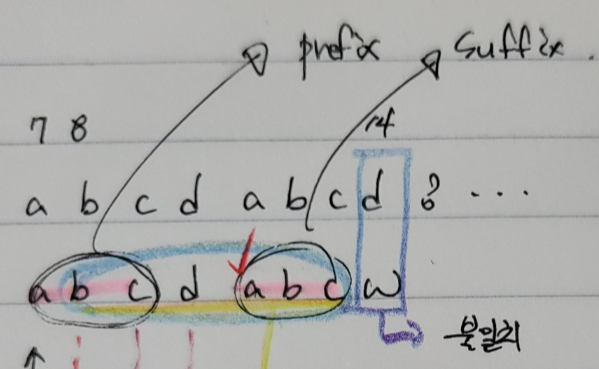
abcdabc에서 prefix, suffix가 같은 값 + suffix(==prefix) 길이가 최대인 길이를 구하면 되는 것입니다.
prefix는
a
ab
abc
abcd
abcda
abcdab
abcdabc
suffix는
c
bc
abc
dabc
cdabc
bcdabc
abcdabc
여기서 prefix == suffix이면서 길이가 가장 큰 경우는 abc d abc 가 있습니다.
kmp 알고리즘의 핵심은 text의 특정 인덱스 i 에서 pattern과 첫 문자가 일치한다면, naive방식과 같이 초기에는 pattern과의 일치 여부를 한 글자씩 순차적으로 비교합니다. 비교 중간에 특정 index i + x 에서 불일치가 발생했을 때! 불일치가 발생하기 전까지는 pattern과의 문자가 전부 일치했던 구간입니다. 이 일치했던 구간을 활용합니다.
i 인덱스부터 불일치하기 전까지, 일치했던 문자열에서 prefix와 suffix를 나눕니다. 위에 처럼요! 그리고 prefix == suffix 같은 경우들을 찾습니다. 그 중에서 가장 큰 문자열 길이에 해당하는 suffix를 시작 지점으로 지정합니다. 이후에 불일치 구간부터 이어서 비교해 나가는 방식입니다.

여기서는 (prefix)abc d abc(suffix). abc suffix가 prefix와 같으면서도 가장 큰 prefix==suffix이기 때문에 이 suffix를 pattern 비교의 시작 위치로 둡니다. 그리고 suffix의 첫 글자인 a부터 시작하는게 아닙니다. suffix의 abc는 이미 패턴 불일치 이전의 기록의 일부에 해당하고 이는 일치 구간이었습니다. text와 일치했던 구간!
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | b | c | d | a | b | c | d |
| a | b | c | d | a | b | c | w |
suffix 의 시작위치인 index 11을 새로운 매칭 지점으로 잡았고 이때 이미 11, 12, 13번째의 정보는 일치했던 구간이었습니다. 굳이 또 비교할 이유가? 이미 불일치 하기 이전! pattern의 substring과 text의 substring이 같은 부분에 대해서 prefix, suffix를 구한 것이었죠.
따라서 text 문자열의 index 11 부터 새로 patterna의 첫 문자와 비교하지 않고 패턴의 비교 위치 시작은 불일치 부분인 d부터! text 또한 시작위치를 11이 아닌 불일치 구간 14부터 14번째부터 차례대로 d a b c w를 비교해 나가면 되는 것입니다.
호호..
정말 신기합니다.
여기서 중요한 키 뽀인트가 있습니다.
정말 중요한 것은 초기에 index 7일 때 text의 문자열 index 7...13까지 그리고 pattern문자열 index 0...6까지 7개의 문자가 동일하다는 점입니다. 이 동일한 문자열을 substring A라고 가정한다면 substring A에서 가장 중요한 것은 prefix와 suffix가 일치하는 게 여러 개 있는데 그 중 가장 큰 녀석을 고른다는게 포인트입니다. 그리고 결국엔 text의 index 7...13과 pattern index 0...6은 서로 같은 문자열입니다. 그래서 결국에 신경써야 할 것은 pattern index 0...6에서 prefix, suffix를 찾는다는 것입니다.
좀 더 살펴보겠습니다.
text : ...?abcdabcd?....
여기서 뒤에 text문장을 늘려보겠습니다.
text: ...?abcdabcdabt?.....
pattern은 여전히 abcdabcw입니다. 주황 밑줄에서 일치 문자를 발견했었고 초록 문자가 suffix에서 가장 길다는 것을 알게 되었습니다. 그리고 이젠 다시 불일치 문자 시점이었던 분홍 밑줄에서 다시 pattern의 특정 문자와 일치하는가를 비교해 나가야 합니다.

또 불일치 구간을 발견했네요. 그렇다면 이번에도
불일치 구간 바로 직전의 문자열 까지를 기준으로 prefix == suffix 를 찾습니다.
abcdab
prefix. suffix 다음 시작은 suffix를 시작으로 해서 불일치 구간을 새롭게 비교해서 탐색해 나갑니다.
중요한 개념이 여기서 있습니다.
text index 7일땐 prefix, suffix를 찾을 때 pattern의 substring은 abcdabc였습니다.
이번엔 abcdab에서 prefix == suffix를 찾았습니다. 만약 불일치 구간이 abcdab 6번째 문자였다면 pattern의 substring abcda에서 prefix == suffix인 a를 찾을 것입니다. 결국엔 주어진 텍스트에서 불일치가 발생하기 전까지는 일치했다는 점이고 이는 pattern의 substring입니다. 무조건! 그렇기에 우리는 pattern에서 prefix == suffix인 길이를 구해 놓는다면 정말 편할 것입니다. 왜냐? 그 이유는 이 문장속에 있기 때문입니다.
만약 text와 비교를 이번엔 pattern의 5번째까지 했을 때 불일치가 발생했다? 그럼 이전까지는 일치였다! abcda (index 4 a에서 불일치) 즉 abcd에서 prefix == suffix를 찾아야 합니다. 존재하지 않습니다.
abcd위치에서
prefix를 아무리 index 1,2,3으로 하든 다 틀리다는 것입니다. 왜? prefix != suffix.
abcd?
a (x)
a (x)
a (x) 결국 시작 위치는 순차적으로 증가하면서 abcd이후의 문자로 넘어가야 합니다.
좋습니다.
결국엔 pattern에서 prefix == suffix인 최대 길이의 정보를 미리 구해 놓는다면 text의 index 0 ~ text.count - pattern.count +1까지 탐색할 때 불일치가 발생했다면 불일치하기 직전에 매칭됬던(일치했던) 문자열 특정 길이에서의 prefix==suffix인 최대 길이 정보를 이용하면 되는 것입니다. text와 불일치가 발생했다면 불일치하기 이전 substring의 길이에 해당하는 정보를 토대로 pi[]를 통해 다음 시작 위치를 어디르 해야 할지 쉽게 알 수 있는 배열 정보를 부분 일치 테이블이라고 합니다.
그 예로 pattern abcdabcw에서의 부분 일치 테이블을 구해본다면

pi = [0,0,0,0,1,2,3,0] 이 구해집니다.
다시다시 처음 설명,, text index7일 pattern과 의 일치여부를 검사할 때로 돌아가서 7,8,9,10,11,12,13까지 7개 문자는 일치했던 문자고 8번째 문자가 일치하지 않았습니다. 그리고 우리는 prefix와 suffix가 abc d abc라는 것을 알았습니다. 그리고 이 정보를 pi에서도 똑같이 구했습니다. pi[7-1] = 3.. // matched된 길이 -1을 할 경우 prefix== suffix 최대 길이를 구할 수 있습니다. 그리고 최대 길이를 이용해서 다음 시작 위치를 가볍게 정할 수 있습니다.
7 + pi[7-1]
prefix의 문자열이 중요한 게 아니라 kmp에선 몇글자가 일치했는지의 여부가 중요합니다.
즉 시작 위치 i를 7이 아닌 i += matched - pi[matched-1] . 7 += 7 - 3
11로 지정하고 matched(일치 수) = pi[matched-1]로 한 후에 불일치 했던 index 14부터 일치했는지 일치하지 않았는지, 일치했다면 일치 수를 증가시키면서~ 답을 찾아가면 됩니다.
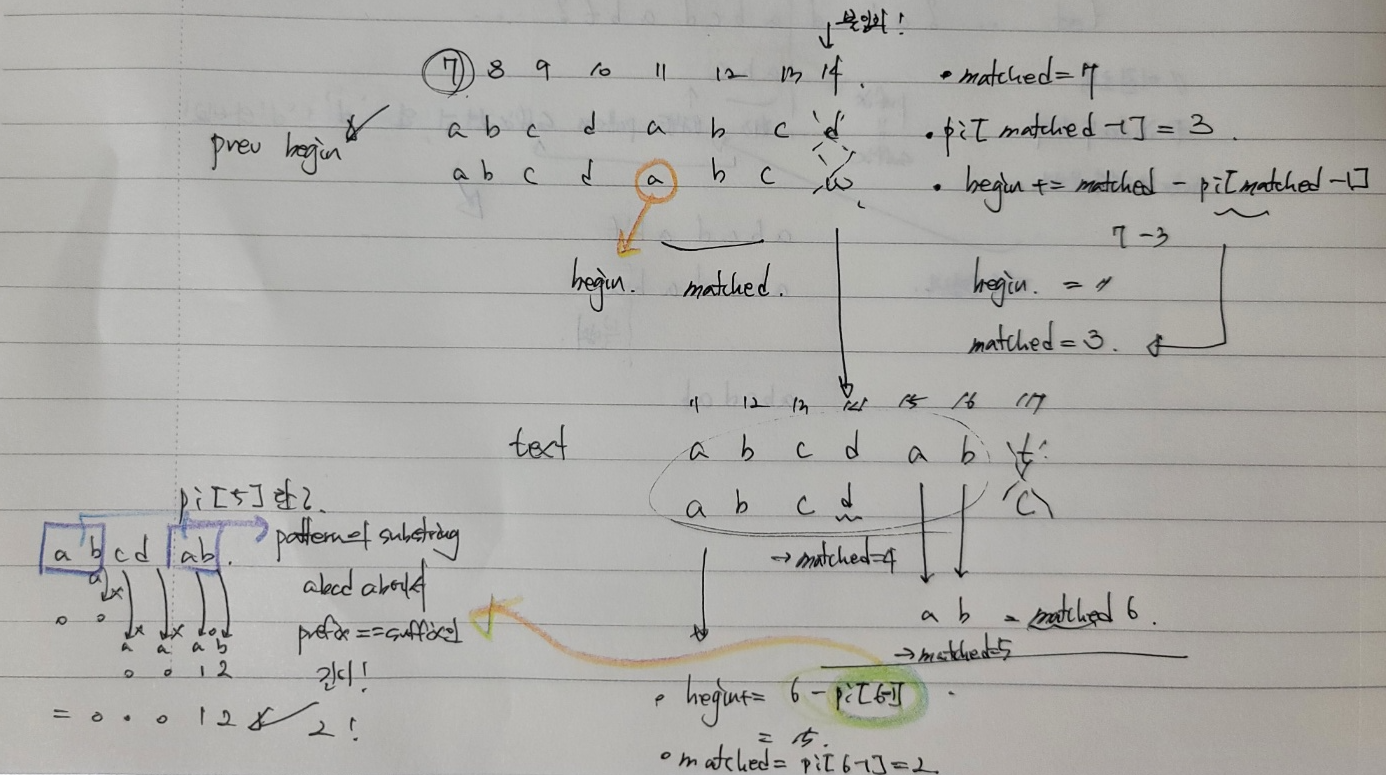
kmp 패턴에서 중요한 것은 pi 부분 일치 테이블을 찾는 것입니다.
특정 pattern일 때 pi찾는 과정을 좀 더 그려봤습니다. 참고해주세요.
Case 1. pattern: ABAABAB

각각의 특정 구간에서,, 예를 들어 ABAA 에서(길이 == 4일 때)의 prefix == suffix 는 A입니다.그리고 matched가 있는 순간 그 다음 글자를 대응합니다. ABAAB
AB(AABAB)
1 2
해당 글자가 대응했으면 그 다 음 글자를 대응합니다.
ABAABAB
ABA(ABAB)
123
일치했으면 또 다음글자를 대응하면서 pi 값을 갱신해나갑니다.
ABAABAB
ABAA(BAB)
x땡! 그 이전까지 일치했던, 카운트 했던 내용을 저장
Case 2. pattern: AABAA
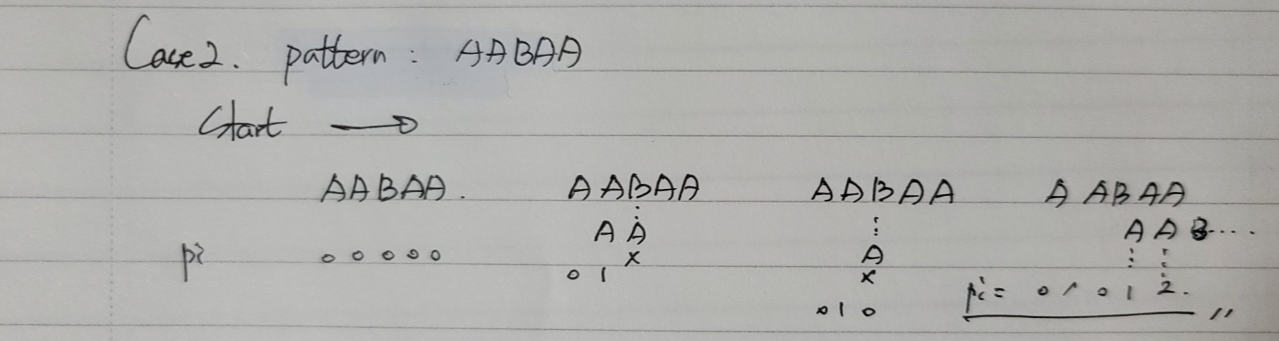
Case 3. pattern: ABACABAAC

이제 prefix, suffix에 따른 pi table을 채울 수 있다면 kmp알고리즘의 개념을 이해하신 것입니다.
이젠 이 모든 글로 작성한 과정을 코드로 도식화 하는 것입니다.
결국 kmp알고리즘에서 중요한 개념은 pi를 찾는 과정인 것 같습니다. kmpSearch은 kmp 알고리즘을 이용해서 text에서 특정 pattern을 찾아 나갑니다. 결론은 pi를 구하기 위해 kmp 알고리즘을 사용하고 text에서 search를 하기 위한 알고리즘으로 kmp 알고리즘을 이용한다...입니다.
정말 신기합니다.
음. .저는 스위프트를 많이 써서 스위프트로 구현했습니다.
/// Setup pi table
getPartialMatch(n: [String]) -> [Int] {
var pi = Array(repeating:0, count: n.count)
var begin = 1, matched = 0
while begin + matched < n.count {
if n[begin+matched] == n[matched] {
matched += 1
pi[begin+matched-1] += matched
} else {
if matched == 0 {
begin += 1
}else {
begin += matched - pi[matched-1]
matched - pi[matched-1]
}
}
return pi
}
/// KMP Algorithm
func kmpSearch() {
let pi = getPartialMatch(n: pattern)
var begin = 0, matched = 0
while begin <= text.count - pattern.count {
if matched<pattern.count && text[begin+matched == pattern[matched] {
matched += 1
if matched == pattern.count {
/// 주어진 text에서 특정 index begin부터 pattern과의 비교가 성공적이었다!
/// 이에대한 결과 로직을 구현하면 됩 니다.
}
}else {
if matched == 0 {
begin += 1
} else {
begin += matched - pi[matched-1]
matched = pi[matched-1]
}
}
}
}
내용중 틀린 부분 발견시 댓글로 알려주신다면 정말 감사합니다..
참고자료:
https://book.algospot.com/
알고리즘 문제 해결 전략
프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략, 구종만 지음, 인사이트, ISBN 978-89-6626-054-6 새 소식 책 소개 <알고리즘 문제 해결 전략>은 새로운 알고리즘 책입니다. 종이에 적힌 의사코드
book.algospot.com
'ComputerScience > Algorithm concepts' 카테고리의 다른 글
| [Algorithm] 플로이드 와셜(Floyd-Warshall) 개념 뿌수기!! (0) | 2023.01.10 |
|---|---|
| [Swift/Algorithm] 우선순위 큐 개념 정리, 최소 힙 개념 with 라이노님 Heap 코드 리뷰 (2) | 2023.01.06 |
| [Algorithm] 그래프의 의미 및 DFS, BFS 탐색 방법 기본 개념 완전 뿌수기!!!! (0) | 2022.09.16 |
| [알고리즘]다익스트라 최단 경로 알고리즘 개념 부수기 / heap이 뭐야? (0) | 2022.08.27 |



